SAM esys-Escript project
Background
esys-Escript is designed as an easy-to-use tool for implementing numerical models using the programming language python. Models can be described through a set of partial differential equations which are solved using the finite element method (FEM) in three dimensions supporting both regular and unstructured meshes. The equations may be time-dependent and non-linear.
When models are coupled esys-Escripts handles the exchange of quantities between the model. For instance, temperature dependent viscosity in the case of temperature driven convection. As no special programming skills are required, esys-Escript is particularly suitable for rapid prototyping.
The user interface provides a high level of abstraction from the underlying discretization methods implemented in C++. Scripts run efficiently on desktop computers as well as massively parallel computers without the need for code redevelopment. Integration with other simulation and data analysis python packages such as numpy, scipy, sympy, matplotlib and pyMC3 are available.
Data can be exchanged with high-end visualization packages and mesh generation tools. esys-Escript has been applied in a broad range of numerical simulations including geomechanics, porous media flow, earth mantle convection, earthquakes, reactive transport, erosion, and tsunamis. To simulate damage propagation in brittle rocks esys-Escript was used to model the weakening of the rocks through small fractures (shown in read) using unstructured finite elements with over 100 Milion cells on 160 cores in mixed OpenMP and MPI mode.
Fracture propagation for axially loaded rock sample (Mondal, Olsen-Kettle & Gross, 2016).
The model consisted of a coupled system of differential equations for rock displacements and the equivalent strain characterising fracturing and was regularized to eliminate mesh dependency.
The equations are solved repeatedly to simulate loading. At each step the material properties of the rock are updated according to a damage evolution relationship.
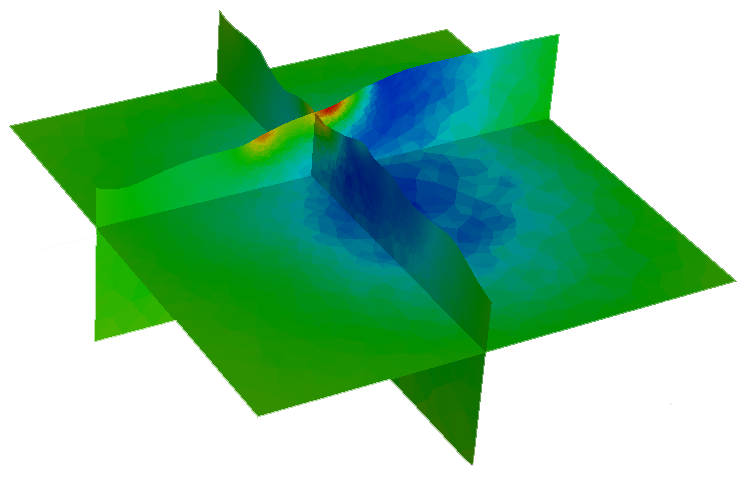
esys-Escript also supports the coupling of models acting on different time scales as found, for example, in seismo-electric coupling. A wave travelling through a porous media can induce an electric field that can be measured on the surface. This is show in the figure below with contour lines representing the wave and the colour spectrum showing the electric field.
Seismic-electric coupled model. The wave is represented by contour lines and the electric field is represented by the colour spectrum (Unpublished; see Shaw & Gross, 2016 for more information).
The signal is particularly strong when the wave passes through interfaces with different electric conductivity and hence the method provides information complementary to seismic recordings. The model is described by a (sonic) wave propagation equation which is coupled with the conservation of current equation to recover the electric field. The simulation is run in esys-escript with the spectral element method for solving the wave equation and the finite element method to model the electric field.
Geophysical data Inversion is a key application area of esys-Escript. Inversion benefits from the tight integration of data analysis tools in python and the fact that esys-Escript is scalable to large number of compute cores. This is a particular advantage over conventional inversion implementations.
Results for three-dimensional inversion of gravity anomaly data in esys-Escript.
Results from electric resistivity tomography (ERT) inversion in esys-Escript.
The inversion strategy employed is tightly integrated with the finite element method, and supports the use of unstructured meshes including available topographical data as shown in the results in the above right figure.
The consistent use of finite element technology in combination with multi-grid driven solvers available in esys-Escript make it possible to run large scale inversion on massive parallel computers. The code has been used to build an Australia's lithospheric density field model and is available through the Auscope geophysicial data portal VGL.
Useful Links
Download esys-Escript: https://esys-escript.github.io
References
Codd & Gross (2018): Electrical resistivity tomography using a finite element based BFGS algorithm with algebraic multigrid preconditioning. Geophysical Journal International, 212 3: 2073-2087.
Liu, Bosco & Suiker (2018): Multi-scale modelling of granular materials: numerical framework and study on micro-structural features Comput Mech.
Schaa, Gross & Plessis (2016): PDE-based geophysical modelling using finite elements: examples from 3D resistivity and 2D magnetotellurics, Journal of Geophysics and Engineering, 13 (2).
Gross & Shaw (2016): Numerical investigations on mapping permeability heterogeneity in coal seam gas reservoirs using seismo-electric methods, Journal of Geophysics and Engineering, Volume 13, Issue 2, 1 April 2016, Pages S50–S58.
Langer, Finzi & Olsen-Kettle (2015): Dynamic triggering of earthquakes is promoted by crustal heterogeneities and bimaterial faults, Physics of the Earth and Planetary Interiors, Volume 238.
Mejia-Herrera, Le Breton, Botella (2014): Solving non-linear PDEs on Gocad models using escript, in: Proc. 34th Gocad Meeting, ASGA.
Guo & Zhao (2014): A coupled FEM/DEM approach for hierarchical multiscale modelling of granular media, Int. J. Numer. Meth. Engng, 99, 789–818.
Gross, Bourgouin, Hale & Muhlhaus (2007): Interface Modeling in Incompressible Media using Level Sets in Escript, Physics of the Earth and Planetary Interiors, 163.
Mondal, Olsen-Kettle & Gross (submitted, 2018): Simulating damage evolution and fracture propagation in sandstone containing a pre-existing 3-D surface flaw under uniaxial compression.
SAM PROGRAM LEADER
Prof. Louis Moresi
Australian National University
ESYS-ESCRIPT PROJECT LEADER
Prof. Lutz Gross
University of Queensland
QUICK LINKS